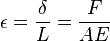jueves, 30 de abril de 2015
sábado, 25 de abril de 2015
UNIDAD N° 10: RESISTENCIA DE MATERIALES - Flexión Simple y Cargas Críticas
PROYECTO G - PUENTE COLGANTE
Canal Encuentro
UNIDAD N°8: RESISTENCIA DE MATERIALES - Ley de Hooke
Ley de elasticidad de Hooke
(Redirigido desde «Ley de Hooke»)
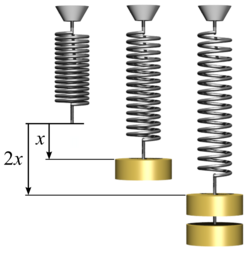
En física, la ley de elasticidad de Hooke o ley de Hooke, originalmente formulada para casos de estiramiento longitudinal, establece que el alargamiento unitario que experimenta un material elástico es directamente proporcional a la fuerza aplicada sobre el mismo
:
:
siendo 
el alargamiento, 
la longitud original, 
: módulo de Young, 
la sección transversal de la pieza estirada. La ley se aplica a materiales elásticos hasta un límite denominado límite elástico.
el alargamiento, la longitud original, : módulo de Young, la sección transversal de la pieza estirada. La ley se aplica a materiales elásticos hasta un límite denominado límite elástico.
Esta ley recibe su nombre de Robert Hooke, físico británico contemporáneo deIsaac Newton, y contribuyente prolífico de la arquitectura. Esta ley comprende numerosas disciplinas, siendo utilizada en ingeniería y construcción, así como en la ciencia de los materiales. Ante el temor de que alguien se apoderara de su descubrimiento, Hooke lo publicó en forma de un famoso anagrama,ceiiinosssttuv, revelando su contenido un par de años más tarde. El anagrama significa Ut tensio sic vis ("como la extensión, así la fuerza").
Link de Wikipedia: https://es.wikipedia.org/wiki/Ley_de_elasticidad_de_Hooke
Video: Introducción a la Elasticidad
Prof. Cesar Antonio Izquierdo Merlo
Ensayo de Tracción
DIAGRAMA DE TENSIÓN DEFORMACIÓN DEL ACERO
viernes, 24 de abril de 2015
UNIDAD N°4: Vínculos y Reacciones de Vínculos
UNIDAD N° 4
VINCULOS Y REACCIONES DE VÍNCULOS
Tareas de la Unidad N°4:
- Leer el Capítulo IX del Libro de Cesar Raffo - Introducción a la Estática de Resistencia de Materiales y realizar el TPN°4.
Ejemplos de Ejercicios resueltos.
EJERCICIO N°1:
1
EJERCICIO N°2:
UNIDAD N°0 EJERCITACION DE ESCALAS. Repaso de trigonometría.
REPASO:
TEOREMA DE PITÁGORAS
Profesor Adrián Paenza, Canal Encuentro.
TEOREMA DE PITÁGORAS
Profesor Adrián Paenza, Canal Encuentro.
Programa de la Materia y Bibliografía
Programa de:
|
T.
P. Estática y resistencia de materiales - AÑO 2015
|
UNIDAD
|
DESARROLLO
|
TRABAJOS PRACTICOS
|
REPASO
|
EJERCITACION
DE ESCALAS Y REPRESENTACIONES DE FUERZAS.
Repaso de trigonometría.
|
T.PNº 0
|
1a
|
METODO GRAFICO:
RESOLUCIÓN DE SISTEMA DE FUERZAS CONCURRENTES.
Composición
Gráfica y analítica de Fuerzas concurrentes con ángulos en los distintos
cuadrantes. Uso de Dinamómetros. Uso del Laboratorio para determinar las componentes
de una fuerza.
|
T.PNº 1
|
1b
|
METODO GRAFICO:
RESOLUCIÓN DE SISTEMA DE FUERZAS NO CONCURRENTES.
POLIGONO FUNICULAR.
Composición gráfica y Analítica de Fuerzas no concurrentes. Polígono
Funicular.
Descomposición de una Fuerza en dos
direcciones paralelas mediante el Polígono Funicular para distintas
posiciones de la fuerza a descomponer respecto de las direcciones paralelas.
|
T.PNº2
|
2
|
MOMENTO DE UNA
FUERZA
Determinación del Momento Estático de una
Fuerza.
Determinación
del Momento Estático de un sistema de fuerzas.
Teorema
de Varignón.
|
T.PNº
3
|
3
|
DESCOMPOSICIÓN DE
FUERZAS-CULMANN Y RITTER
Descomposición
analítica de una fuerza en dos direcciones paralelas,
Composición
de pares. Uso del Laboratorio para determinar el par de fuerzas.
Composición
de un Par y una Fuerza.
Descomposición
de una fuerza en dos direcciones concurrentes con ella. Calculo Gráfico y
analítico. Uso del Laboratorio para la determinación de Fuerzas Coplanarias
Concurrentes. Descomposición de una Fuerza en Tres Direcciones. Método de
Cullman y Ritter
|
T.PNº 4
|
4
|
VINCULOS Y
REACCIONES DE VÍNCULOS
Análisis de Estructuras, tipos de Vínculos
y Reacciones de Vínculos.
|
T.PNº 5
|
5
|
CENTRO
DE GRAVEDAD
Calculo Gráfico y Analítico de Baricentros de Figuras simples y compuestas.
Perfiles L, T, U y Z.
|
T.PNº 6
T.P Grupal
Baricentro de piezas
|
6
|
MOMENTO
DE INERCIA
Calculo Gráfico y Analítico de Momentos de
Inercia de perfiles. Uso del Laboratorio para la determinación del Momento de
Inercia.
Calculo
Analítico de módulos resistentes respecto de ejes baricéntricos, del
cuadrado, rectángulo, círculo.
Teorema de Steiner.
|
T.PNº 7
|
7
|
DIAGRAMAS
CARACTERÍSTICOS, MOMENTO FLECTOR, CORTE Y ESFUERZO NORMAL.
Determinación de los tres diagramas característicos
para el análisis de la estructura..
|
T.PNº 8
T.P Grupal
Ensayos de materiales
|
8
|
RESISTENCIA
DE MATERIALES: LEY DE HOOKE
Determinación de esfuerzos de tensión en
distintos materiales.
Uso del laboratorio para la obtención de valores de tracción y
compresión.
Calculo de tensiones admisibles. Uso de tablas de valores obtenidos
empíricamente.
Determinación de esfuerzos de Flexión en vigas de diferentes tamaños y
materiales.
Determinación de deformaciones. Principio
de Independencia de Acciones y superposición de efectos.
Principio de Bernoulli o de Navier.
|
T.PNº 9
|
9
|
RESISTENCIA
DE MATERIALES: TRACCION Y COMPRESION SIMPLE
Clasificación de los aceros. Obtención del
Modulo de Elasticidad.
Uso del Laboratorio para la determinación de constante de resorte y
otros cuerpos elásticos. Relación esfuerzos deformaciones. Alargamiento a la
rotura. Estricción.
Influencia del peso propio y de la temperatura.
|
T.PNº 9
|
10
|
RESISTENCIA
DE MATERIALES: FLEXION SIMPLE CARGAS CRITICAS
Ecuaciones de estabilidad. Cálculo de las secciones resistentes.
Determinación del perfil
Concepto de pandeo. Cargas críticas. Fórmula de Euler. Esbeltez.
Tensión crítica. Efectos de pandeo en piezas de madera. Verificación y diseño
de columnas. Perfiles compuestos. CREMONA
|
T.PNº 10
T.P Grupal
Estructuras con fideos
|
Bibliografía:
Cesar M. Raffo, Introducción a la Estática y Resistencia de Materiales, 11° Edición, Librería y Editorial Alsina, 2007. 304p.
Suscribirse a:
Entradas (Atom)